
All categories
Featured selections
Trade Assurance
Buyer Central
Help Center
Get the app
Become a supplier

(4549 productos disponibles)









































En matemáticas, una **función lineal** es una función que grafica una línea recta. Tiene una tasa de cambio constante. Las funciones lineales a menudo se escriben en la forma f(x) = mx + b, donde m y b son constantes. En este caso, m es la pendiente de la línea, mientras que b es la intersección con el eje y. Las funciones lineales tienen varios tipos, que incluyen:
Función lineal de identidad
Este es el tipo más básico de función lineal. Las funciones lineales de identidad tienen la misma pendiente e intersección con el eje y de 0. Se escriben como f(x)=x o 1x.
Función lineal constante
Las funciones lineales constantes tienen una pendiente de cero. Son líneas horizontales en una gráfica. No importa qué valor de entrada se proporcione, la salida siempre es la misma.
Función lineal decreciente
Una función lineal decreciente tiene una pendiente negativa. A medida que el valor de entrada aumenta, el valor de salida disminuye. La línea en la gráfica se inclina hacia abajo de izquierda a derecha.
Función lineal creciente
Una función lineal creciente tiene una pendiente positiva. A medida que el valor de entrada aumenta, el valor de salida también aumenta. La línea de la gráfica se inclina hacia arriba de izquierda a derecha.
Función escalonada
Una función escalonada es una función constante por partes. Su gráfica consta de una serie de segmentos de línea horizontales. Cada segmento representa un valor constante en un intervalo.
Función lineal inversa
Una función lineal inversa es una reflexión de una función lineal a través de la línea y=x. Por ejemplo, una función lineal creciente tendrá una función lineal decreciente como su inversa.
Función afín
Una función afín es una función lineal que no necesariamente pasa por el origen. Puede tener una intersección con el eje y diferente de cero.
Funciones cuadráticas
Estas no son funciones lineales. Sin embargo, pueden ser funciones lineales en un cierto intervalo. Por ejemplo, las funciones cuadráticas pueden ser funciones lineales en su vértice.
Comprender las especificaciones y el mantenimiento de una función lineal es crucial para garantizar su aplicación exitosa en diversos contextos.
Estos son algunos puntos clave a tener en cuenta:
Los compradores mayoristas necesitan comprender los diferentes aspectos de las funciones lineales para poder elegir la mejor. Estos son los factores a considerar al elegir funciones lineales:
Propósito
Se debe considerar el propósito de la función lineal. ¿Qué quiere lograr el comprador? ¿Obtener los valores de salida o encontrar la pendiente de la función? Dependiendo del propósito, se elegirá una función lineal adecuada.
Facilidad de uso
Los compradores de piezas deben considerar qué tan fácil será usar la función lineal. Especialmente si quieren usarlo para fines educativos, deben elegir uno que sea simple y fácil de entender.
Flexibilidad
Considere si la función lineal es flexible o no. Si se puede ajustar o cambiar en función de diferentes situaciones o requisitos, será más útil en varios contextos.
Compatibilidad
Los compradores de negocios deben asegurarse de que la función lineal que elijan sea compatible con otras herramientas, métodos o marcos que están utilizando. Esto facilitará la integración y hará que la función sea más efectiva.
Soporte y documentación
Verifique si hay suficiente soporte y documentación disponibles para la función lineal elegida. Esto puede incluir guías del usuario, ejemplos, tutoriales o soporte de la comunidad. Tener estos recursos puede ayudar a comprender y utilizar la función de manera efectiva.
Aquí se explica cómo hacer bricolaje y reemplazar una función lineal.
P1: ¿Dónde se utilizan los actuadores lineales?
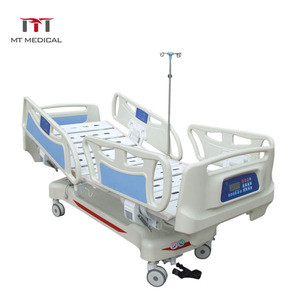
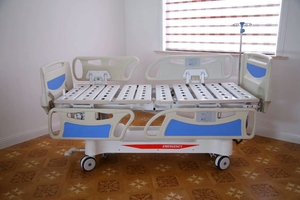
R1: Los actuadores lineales se utilizan ampliamente en diversas industrias y aplicaciones. Algunos ejemplos incluyen: Manufactura: Los actuadores lineales se utilizan en líneas de ensamblaje para tareas automatizadas como levantar, empujar y posicionar artículos. Salud: El equipo médico, como las camas de hospital y las mesas de examen, utiliza actuadores lineales para el ajuste de altura y la comodidad del paciente. Robótica: Los actuadores lineales se utilizan en robots para movimientos precisos, como recoger y colocar artículos en la fabricación o la logística. Automotriz: Los actuadores lineales se utilizan en diversas aplicaciones automotrices, como asientos ajustables, abridores de maletero y sistemas de control del motor. Aeroespacial: Los actuadores lineales se utilizan en aviones para diversas superficies de control, como alerones, lamas y operaciones de tren de aterrizaje.
P2: ¿Cuáles son las ventajas de los actuadores lineales?
R2: Los actuadores lineales ofrecen varias ventajas que los hacen adecuados para diversas aplicaciones que requieren movimiento lineal. Algunas de estas ventajas incluyen: Precisión y exactitud: Los actuadores lineales proporcionan un control preciso y exacto del movimiento lineal, lo que los hace adecuados para aplicaciones que requieren alta precisión, como tareas de posicionamiento y medición. Alta fuerza y capacidad de carga: Los actuadores lineales pueden generar una fuerza significativa y manejar cargas pesadas, lo que los hace adecuados para aplicaciones que involucran manejo de materiales, elevación y tareas de empuje. Fiabilidad y durabilidad: Los actuadores lineales están diseñados para ser robustos y duraderos, lo que garantiza un rendimiento confiable y duradero incluso en entornos industriales exigentes. Flexibilidad y versatilidad: Los actuadores lineales se pueden configurar y personalizar para adaptarse a los requisitos específicos de la aplicación, como la longitud de carrera, la velocidad, la fuerza y la interfaz de control. Esto los hace adecuados para diversas aplicaciones en diferentes industrias.
P3: ¿Cuáles son las características de un actuador lineal?
R3: Los actuadores lineales tienen varias características importantes que les permiten realizar tareas de movimiento lineal preciso y controlado. Estas características incluyen: Movimiento controlado: Los actuadores lineales proporcionan un movimiento controlado a lo largo de una línea recta, lo que permite tareas como empujar, tirar, levantar o posicionar objetos con precisión. Parámetros de movimiento: Los actuadores lineales tienen características que permiten el control sobre los parámetros de movimiento, como la longitud de carrera, la velocidad y la fuerza. Esto permite la personalización y el ajuste de acuerdo con los requisitos específicos de la aplicación. Interfaz de control: Los actuadores lineales están equipados con interfaces de control como digitales, analógicas o protocolos de comunicación. Esto permite la integración con sistemas de control, lo que permite el control remoto, la automatización y la sincronización del movimiento lineal con otros procesos. Retroalimentación y monitoreo: Algunos actuadores lineales tienen características integradas de retroalimentación y monitoreo, como sensores de posición o sensores de fuerza. Estas características brindan retroalimentación en tiempo real sobre el rendimiento del actuador, lo que permite el control de lazo cerrado, el monitoreo y el diagnóstico de tareas de movimiento lineal.













































































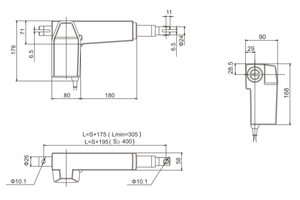


























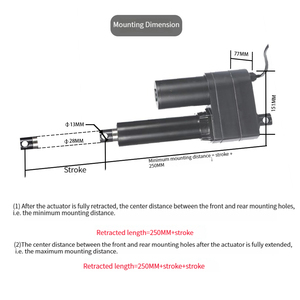














































En matemáticas, una **función lineal** es una función que grafica una línea recta. Tiene una tasa de cambio constante. Las funciones lineales a menudo se escriben en la forma f(x) = mx + b, donde m y b son constantes. En este caso, m es la pendiente de la línea, mientras que b es la intersección con el eje y. Las funciones lineales tienen varios tipos, que incluyen:
Función lineal de identidad
Este es el tipo más básico de función lineal. Las funciones lineales de identidad tienen la misma pendiente e intersección con el eje y de 0. Se escriben como f(x)=x o 1x.
Función lineal constante
Las funciones lineales constantes tienen una pendiente de cero. Son líneas horizontales en una gráfica. No importa qué valor de entrada se proporcione, la salida siempre es la misma.
Función lineal decreciente
Una función lineal decreciente tiene una pendiente negativa. A medida que el valor de entrada aumenta, el valor de salida disminuye. La línea en la gráfica se inclina hacia abajo de izquierda a derecha.
Función lineal creciente
Una función lineal creciente tiene una pendiente positiva. A medida que el valor de entrada aumenta, el valor de salida también aumenta. La línea de la gráfica se inclina hacia arriba de izquierda a derecha.
Función escalonada
Una función escalonada es una función constante por partes. Su gráfica consta de una serie de segmentos de línea horizontales. Cada segmento representa un valor constante en un intervalo.
Función lineal inversa
Una función lineal inversa es una reflexión de una función lineal a través de la línea y=x. Por ejemplo, una función lineal creciente tendrá una función lineal decreciente como su inversa.
Función afín
Una función afín es una función lineal que no necesariamente pasa por el origen. Puede tener una intersección con el eje y diferente de cero.
Funciones cuadráticas
Estas no son funciones lineales. Sin embargo, pueden ser funciones lineales en un cierto intervalo. Por ejemplo, las funciones cuadráticas pueden ser funciones lineales en su vértice.
Comprender las especificaciones y el mantenimiento de una función lineal es crucial para garantizar su aplicación exitosa en diversos contextos.
Estos son algunos puntos clave a tener en cuenta:
Los compradores mayoristas necesitan comprender los diferentes aspectos de las funciones lineales para poder elegir la mejor. Estos son los factores a considerar al elegir funciones lineales:
Propósito
Se debe considerar el propósito de la función lineal. ¿Qué quiere lograr el comprador? ¿Obtener los valores de salida o encontrar la pendiente de la función? Dependiendo del propósito, se elegirá una función lineal adecuada.
Facilidad de uso
Los compradores de piezas deben considerar qué tan fácil será usar la función lineal. Especialmente si quieren usarlo para fines educativos, deben elegir uno que sea simple y fácil de entender.
Flexibilidad
Considere si la función lineal es flexible o no. Si se puede ajustar o cambiar en función de diferentes situaciones o requisitos, será más útil en varios contextos.
Compatibilidad
Los compradores de negocios deben asegurarse de que la función lineal que elijan sea compatible con otras herramientas, métodos o marcos que están utilizando. Esto facilitará la integración y hará que la función sea más efectiva.
Soporte y documentación
Verifique si hay suficiente soporte y documentación disponibles para la función lineal elegida. Esto puede incluir guías del usuario, ejemplos, tutoriales o soporte de la comunidad. Tener estos recursos puede ayudar a comprender y utilizar la función de manera efectiva.
Aquí se explica cómo hacer bricolaje y reemplazar una función lineal.
P1: ¿Dónde se utilizan los actuadores lineales?
R1: Los actuadores lineales se utilizan ampliamente en diversas industrias y aplicaciones. Algunos ejemplos incluyen: Manufactura: Los actuadores lineales se utilizan en líneas de ensamblaje para tareas automatizadas como levantar, empujar y posicionar artículos. Salud: El equipo médico, como las camas de hospital y las mesas de examen, utiliza actuadores lineales para el ajuste de altura y la comodidad del paciente. Robótica: Los actuadores lineales se utilizan en robots para movimientos precisos, como recoger y colocar artículos en la fabricación o la logística. Automotriz: Los actuadores lineales se utilizan en diversas aplicaciones automotrices, como asientos ajustables, abridores de maletero y sistemas de control del motor. Aeroespacial: Los actuadores lineales se utilizan en aviones para diversas superficies de control, como alerones, lamas y operaciones de tren de aterrizaje.
P2: ¿Cuáles son las ventajas de los actuadores lineales?
R2: Los actuadores lineales ofrecen varias ventajas que los hacen adecuados para diversas aplicaciones que requieren movimiento lineal. Algunas de estas ventajas incluyen: Precisión y exactitud: Los actuadores lineales proporcionan un control preciso y exacto del movimiento lineal, lo que los hace adecuados para aplicaciones que requieren alta precisión, como tareas de posicionamiento y medición. Alta fuerza y capacidad de carga: Los actuadores lineales pueden generar una fuerza significativa y manejar cargas pesadas, lo que los hace adecuados para aplicaciones que involucran manejo de materiales, elevación y tareas de empuje. Fiabilidad y durabilidad: Los actuadores lineales están diseñados para ser robustos y duraderos, lo que garantiza un rendimiento confiable y duradero incluso en entornos industriales exigentes. Flexibilidad y versatilidad: Los actuadores lineales se pueden configurar y personalizar para adaptarse a los requisitos específicos de la aplicación, como la longitud de carrera, la velocidad, la fuerza y la interfaz de control. Esto los hace adecuados para diversas aplicaciones en diferentes industrias.
P3: ¿Cuáles son las características de un actuador lineal?
R3: Los actuadores lineales tienen varias características importantes que les permiten realizar tareas de movimiento lineal preciso y controlado. Estas características incluyen: Movimiento controlado: Los actuadores lineales proporcionan un movimiento controlado a lo largo de una línea recta, lo que permite tareas como empujar, tirar, levantar o posicionar objetos con precisión. Parámetros de movimiento: Los actuadores lineales tienen características que permiten el control sobre los parámetros de movimiento, como la longitud de carrera, la velocidad y la fuerza. Esto permite la personalización y el ajuste de acuerdo con los requisitos específicos de la aplicación. Interfaz de control: Los actuadores lineales están equipados con interfaces de control como digitales, analógicas o protocolos de comunicación. Esto permite la integración con sistemas de control, lo que permite el control remoto, la automatización y la sincronización del movimiento lineal con otros procesos. Retroalimentación y monitoreo: Algunos actuadores lineales tienen características integradas de retroalimentación y monitoreo, como sensores de posición o sensores de fuerza. Estas características brindan retroalimentación en tiempo real sobre el rendimiento del actuador, lo que permite el control de lazo cerrado, el monitoreo y el diagnóstico de tareas de movimiento lineal.